PARADOKS BANACH-TARSKI

Keanehan dalam matematika tidaklah sedikit. Dalam artikel ini diperkenalkan salah satu teori matematika yang menarik untuk kita ketahui. Teori ini berkaitan dengan salah satu objek dalam R³. Bisa dibilang ini adalah yang paling mustahil, paling aneh, dan paling ajaib dalam matematika. Menurut Paradoks Banach-Tarski, kita bisa memecahkan bola padat menjadi kepingan- kepingan berhingga kemudian menyusun ulang kepingan-kepingan tsb dengan menggunakan rotasi, dan translasi menjadi 2 buah bola yang identik dengan sebelumnya. Perlu dipahami bahwa bola padat yang dimaksudkan disini adalah bola padat menurut pemahaman matematika yaitu himpunan titik-titik tak hingga yang didefinisikan sebagai

dengan r jari-jari bola. Teori yang ditemukan oleh Stefan Banach dan Alfred Tarski ini melibatkan beberapa teori sebelumnya yaitu Translasi, rotasi, isometri, kongruen dan aksioma pilihan.

Paradox Banach-Tarski (PBT) dijelaskan dalam dua versi yaitu versi lemah dan versi kuat. Kedua versi ini memperlihatkan keanehan, dan keajaiban yang berbeda.

Versi Lemah

Proses PBT yang dijelaskan dalam versi ini mempertahankan: Bentuk, Ukuran, Kepadatan, dan Volume.

· Bentuk, artinya setelah proses PBT berlangsung bola padat yang dihasilkan sama seperti bola padat sebelumnya, tidak menjadi lonjong, gepeng atau setengah bola.

· Ukuran, artinya jika bola padat yang dipecah berjari-jari r, maka hasil PBT akan tetap berjari-jari r juga.

· Kepadatan, artinya untuk mendapatkan dua atau lebih bola padat yang memiliki ukuran dan bentuk yang sama dari susunan pecahan sebuah bola padat, tidak dilakukan peregangan, sehingga kepadatannya tetap.

· Volume, artinya tidak dilakukan penambahan material kepingan dari luar kepingan sebuah bola padat sebelumnya.

Untuk lebih jelasnya, perhatikan analogi berikut :

Secara formal, PBT Versi Lemah ini mengatakan,

Untuk sebarang bola padat

dapat dipecahkan menjadi kepingan-kepingan berhingga
dan isometri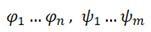
R³ sedemikian sehingga

Versi Kuat

Disini PBT hanya mempertahankan: Bentuk,dan Kepadatan.

Untuk volume dan ukuran tidak dipertahankan, namun bukan berarti versi ini tidak lebih aneh dari versi kuat. Untuk penjelasan mempertahankan bentuk dan kepadatan sama dengan di atas. Analogi berikut akan membantu Anda untuk menjadi lebih yakin bahwa versi ini memang pantas dikatakan versi kuat.

(sebuah kelereng)

=> (Matahari)

Sangat mustahil bukan ?

Percaya atau tidak, didunia matematika itu sangat mungkin dengan menggunakan PBT versi ini.

Versi kuat PBT mengatakan,

Untuk sebarang dua bola padat A dan B dengan
maka dapat dipecah menjadi kepingan-kepingan berhingga
dan

sedemikian sehingga untuk setiap i dari 1 sampai n,A_i kongruen dengan B_i. Perlu diketahui bahwa PBT ini tidak berlaku di R dan R². Dan beberapa literature mengatakan bahwa PBT akan dapat terjadi jika banyak kepingan tidak kurang dari 4 kepingan.

by Departement Saintek