SELAMAT KEPADA PARA PEMENANG MATHEMATIC CHALLENGE 2012

Read More

MATEMATIKA DAN BILANGAN PRIMA

Bilangan prima adalah dasar dari matematika, termasuk salah satu misteri alam semesta. Tidak pernah terbayangkan oleh manusia sebelumnya, sampai ditemukan bahwa bilangan prima juga merupakan dasar dari kehidupan alam, yang dengan usaha keras ingin dijelaskan oleh ilmu ini dalam sains. Pandangan orang umumnya mengatakan bahwa matematika hanyalah penemuan manusia biasa. Sebaliknya, beberapa pemikir masa lalu - Pythagoras, Plato, Cusanus, Kepler, Leibnitz, Newton, Euler, Gauss, termasuk para revolusioner abad ke-20, Planck, Einstein dan Sommerffeld - yakin bahwa keberadaan angka dan bentuk geometris merupakan konsep alam semesta dan konsep yang bebas (independent). Galileo sendiri beranggapan bahwa matematika adalah bahasa Tuhan ketika menulis alam semesta.

Bilangan Prima dan Rencana Penciptaan
Salah satu teka-teki lama yang belum sepenuhnya terpecahkan adalah bilangan prima. Bilangan prima adalah bilangan yang hanya dapat habis dibagi oleh bilangan itu sendiri dan angka 1. Angka 12 bukan merupakan bilangan prima, karena dapat habis dibagi oleh angka lainnya 2, 3, dan 4. Bilangan prima adalah 2, 3, 5, 7, 11, 13, .... dan seterusnya. Banyak bilangan prima tidak terhingga. Tidak peduli berapa banyak kita menghitung, pasti kita akan menemukan bilangan prima, walaupun mungkin makin jarang_ Hal ini menjadi teka-teki kita, jika kita ingat bilangan ini tidak dapat dibagi oleh angka lainnya. Salah satu hal yang menakjubkan, dalam era komputer kita memberikan kodetifikasi semua hal yang penting dan rahasia, di bank, asuransi, dan perhitungan-perhitungan peluru kendali, security system dengan enkripsi, dalam angka jutaan bilangan-bilangan yang tidak habis dibagi oleh angka lainnya. Ini diperlukan karena dengan penggunaan angka lain, kodetifikasi tadi dapat dengan mudah ditembus.

Fenomena inilah yang ditemukan ilmuwan dari Duesseldorf (Dr. Plichta), sehubungan dengan penciptaan alam, yaitu distribusi misterius bilangan prima. Para ilmuwan sudah lama percaya bahwa bilangan prima adalah bahasa universal yang dapat dimengerti oleh semua makhluk (spesies) berintelegensia tinggi, sebagai komunikasi dasar antarmereka. Bahasa ini penuh misteri karena berhubungan dengan perencanaan universal kosmos.

Bilangan lain yang perlu diketahui adalah sisa dari bilangan prima, yakni bilangan komposit, kecuali angka 1, yaitu 4, 6, 8, 9,10,12,14,15, .... dan seterusnya. Dengan kata lain, bilangan komposit adalah bilangan yang terdiri dari minimal dua faktor prima. Misalnya :

6 = 2 x 3 = 2 . 3
30 = 2 x 3 x 5 = 2 . 3 . 5
85 = 5 x 17 = 5 . 17

Selain itu, dikenal pula bilangan khusus, yang disebut prima kembar, yaitu bilangan prima yang angkanya berdekatan dengan selisih 2. Misalnya :
(3,5)
(5,7)
(11,13)
(17,19)
dan seterusnya.
Mayoritas ahli astrofisika juga percaya bahwa di alam semesta terdapat  "kode kosmos"  atau yang disebut cosmic code based on this order,  yang dikenal juga sebagai Theory of Everything (TOE), yang artinya terdapat konstanta-konstanta alam semesta yang saling berhubungan berdasarkan perintah pendesain. Sekali perintah tersebut dapat dipecahkan, maka hal ini akan membuka pandangan sains lainnya yang berhubungan.

MISTERI  BILANGAN NOL

Ratusan tahun yang lalu, manusia hanya mengenal 9 lambang bilangan yakni 1, 2, 2, 3, 5, 6, 7, 8, dan 9. Kemudian, datang angka 0, sehingga jumlah lambang bilangan menjadi 10 buah. Tidak diketahui siapa pencipta bilangan 0, bukti sejarah hanya memperlihatkan bahwa bilangan 0 ditemukan pertama kali dalam zaman Mesir kuno. Waktu itu bilangan nol hanya sebagai lambang. Dalam zaman modern, angka nol digunakan tidak saja sebagai lambang, tetapi juga sebagai bilangan yang turut serta dalam operasi matematika. Kini, penggunaan bilangan nol telah menyusup jauh ke dalam sendi kehidupan manusia. Sistem berhitung tidak mungkin lagi mengabaikan kehadiran bilangan nol, sekalipun bilangan nol itu membuat kekacauan logika. Mari kita lihat.

Nol, penyebab komputer macet

Pelajaran tentang bilangan nol, dari sejak zaman dahulu sampai sekarang selalu menimbulkan kebingungan bagi para pelajar dan mahasiswa, bahkan masyarakat pengguna. Mengapa? Bukankah bilangan nol itu mewakili sesuatu yang tidak ada dan yang tidak ada itu ada, yakni nol. Siapa yang tidak bingung? Tiap kali bilangan nol muncul dalam pelajaran Matematika selalu ada ide yang aneh. Seperti ide jika sesuatu yang ada dikalikan dengan 0 maka menjadi tidak ada. Mungkinkah 5*0 menjadi tidak ada? (* adalah perkalian). Ide ini membuat orang frustrasi. Apakah nol ahli sulap?

Lebih parah lagi-tentu menambah bingung-mengapa 5+0=5 dan 5*0=5 juga? Memang demikian aturannya, karena nol dalam perkalian merupakan bilangan identitas yang sama dengan 1. Jadi 5*0=5*1. Tetapi, benar juga bahwa 5*0=0. Waw. Bagaimana dengan 5^o=1, tetapi 50^o=1 juga? Ya, sudahlah. Aturan lain tentang nol yang juga misterius adalah bahwa suatu bilangan jika dibagi nol tidak didefinisikan. Maksudnya, bilangan berapa pun yang tidak bisa dibagi dengan nol. Komputer yang canggih bagaimana pun akan mati mendadak jika tiba-tiba bertemu dengan pembagi angka nol. Komputer memang diperintahkan berhenti berpikir jika bertemu sang divisor nol.

Bilangan nol: tunawisma

Bilangan disusun berdasarkan hierarki menurut satu garis lurus. Pada titik awal adalah bilangan nol, kemudian bilangan 1, 2, dan seterusnya. Bilangan yang lebih besar di sebelah kanan dan bilangan yang lebih kecil di sebelah kiri. Semakin jauh ke kanan akan semakin besar bilangan itu. Berdasarkan derajat hierarki (dan birokrasi bilangan), seseorang jika berjalan dari titik 0 terus-menerus menuju angka yang lebih besar ke kanan akan sampai pada bilangan yang tidak terhingga. Tetapi, mungkin juga orang itu sampai pada titik 0 kembali. Bukankah dunia ini bulat? Mungkinkah? Bukankah Columbus mengatakan bahwa kalau ia berlayar terus-menerus ia akan sampai kembali ke Eropa?

Lain lagi. Jika seseorang berangkat dari nol, ia tidak mungkin sampai ke bilangan 4 tanpa melewati terlebih dahulu bilangan 1, 2, dan 3. Tetapi, yang lebih aneh adalah pertanyaan mungkinkan seseorang bisa berangkat dari titik nol? Jelas tidak bisa, karena bukankah titik nol sesuatu titik yang tidak ada? Aneh dan sulit dipercaya? Mari kita lihat lebih jauh.

Jika di antara dua bilangan atau antara dua buah titik terdapat sebuah ruas. Setiap bilangan mempunyai sebuah ruas. Jika ruas ini dipotong-potong kemudian titik lingkaran hitam dipindahkan ke tengah-tengah ruas, ternyata bilangan 0 tidak mempunyai ruas. Jadi, bilangan nol berada di awang-awang. Bilangan nol tidak mempunyai tempat tinggal alias tunawisma. Itulah sebabnya, mengapa bilangan nol harus menempel pada bilangan lain, misalnya, pada angka 1 membentuk bilangan 10, 100, 109, 10.403 dan sebagainya. Jadi, seseorang tidak pernah bisa berangkat dari angka nol menuju angka 4. Kita harus berangkat dari angka 1.

Mudah, tetapi salah

Guru meminta Ani menggambarkan sebuah garis geometrik dari persamaan 3x+7y = 25. Ani berpikir bahwa untuk mendapatkan garis itu diperlukan dua buah titik dari ujung ke ujung. Tetapi, setelah berhitung-hitung, ternyata cuma ada satu titik yang dilewati garis itu, yakni titik A(6, 1), untuk x=6 dan y=1. Sehingga Ani tidak bisa membuat garis itu. Sang guru mengingatkan supaya menggunakan bilangan nol. Ya, itulah jalan keluarnya. Pertama, berikan y=0 diperoleh x=(25-0)/3=8 (dibulatkan), merupakan titik pertama, B(8,0). Selanjutnya berikan x=0 diperoleh y=(25-3.0)/7=4 (dibulatkan), merupakan titik kedua C(0,4). Garis BC, adalah garis yang dicari. Namun, betapa kecewanya sang guru, karena garis itu tidak melalui titik A. Jadi, garis BC itu salah.

Ani membela diri bahwa kesalahan itu sangat kecil dan bisa diabaikan. Guru menyatakan bahwa bukan kecil besarnya kesalahan, tetapi manakah yang benar? Bukankah garis BC itu dapat dibuat melalui titik A? Kata guru, gunakan bilangan nol dengan cara yang benar. Bagaimana kita harus membantu Ani membuat garis yang benar itu? Mudah, kata konsultan Matematika. Mula-mula nilai 25 dalam 3x+7y harus diganti dengan hasil perkalian 3 dan 7 sehingga diperoleh 3x+7y=21.

Selanjutnya, dalam persamaan yang baru, berikan y=0 diperoleh x=21/3=7 (tanpa pembulatan) itulah titik pertama P(6,1). Kemudian berikan nilai x=0 diperoleh y=21/7 = 3 (tanpa pembulatan), itulah titik kedua Q(0, 3). Garis PQ adalah garis yang sejajar dengan garis yang dicari, yakni 3x+7y=25. Melalui titik A tarik garis sejajar dengan PQ diperoleh garis P1Q1. Nah, begitulah. Sang murid telah menemukan garis yang benar berkat bantuan bilangan nol.

Akan tetapi, sang guru masih sangat kecewa karena sebenarnya tidak ada satu garis pun yang benar. Bukankah dalam persamaan 3x1+7x2=25 hanya ada satu titik penyelesaian yakni titik A, yang berarti persamaan 3x1+7x2 itu hanya berbentuk sebuah titik? Bahkan pada persamaan 3x1+7x2=21 tidak ada sebuah titik pun yang berada dalam garis PQ. Oleh karena itu, garis PQ dalam sistem bilangan bulat, sebenarnya tidak ada. Aneh, bilangan nol telah menipu kita. Begitulah kenyataannya, sebuah persamaan tidak selalu berbentuk sebuah garis.

Bergerak, tetapi diam

Bilangan tidak hanya terdiri atas bilangan bulat, tetapi juga ada bilangan desimal antara lain dari 0,1; 0,01; 0,001; dan seterusnya sekuat-kuat kita bisa menyebutnya sampai sedemikian kecilnya. Karena sangat kecil tidak bisa lagi disebut atau tidak terhingga dan pada akhirnya dianggap nol saja. Tetapi, ide ini ternyata sempat membingungkan karena jika bilangan tidak terhingga kecilnya dianggap nol maka berarti nol adalah bilangan terkecil? Padahal, nol mewakili sesuatu yang tidak ada? Waw. Begitulah.

Berdasarkan konsep bilangan desimal dan kontinu, maka garis bilangan yang kita pakai ternyata tidak sesederhana itu karena antara dua bilangan selalu ada bilangan ke tiga. Jika seseorang melompat dari bilangan 1 ke bilangan 2, tetapi dengan syarat harus melompati terlebih dahulu ke bilangan desimal yang terdekat, bisakah? Berapakah bilangan desimal terdekat sebelum sampai ke bilangan 2? Bisa saja angka 1/2. Tetapi, anda tidak boleh melompati ke angka 1/2 karena masih ada bilangan yang lebih kecil, yakni 1/4. Seterusnya selalu ada bilangan yang lebih dekat... yakni 0,1 lalu ada 0,01, 0,001, ..., 0,000001. demikian seterusnya, sehingga pada akhirnya bilangan yang paling dekat dengan angka 1 adalah bilangan yang demikian kecilnya sehingga dianggap saja nol. Karena bilangan terdekat adalah nol alias tidak ada, maka Anda tidak pernah bisa melompat ke bilangan 2?

Disadur dari: http://www.duniaesai.com/sains/sains16.htm

MENUJU KE ABSTRAK

Pemahaman akan pengertian abstrak sepertinya masih dianggap sebagai suatu yang sulit bahkan tak teraplikasi. Bagi orang di pinggir jalan, boleh jadi menganggap orang yang belajar matematika abstrak sebagai orang sinting.

     Saatnya kita harus menguak apa yang dimaksud abstrak dalam matematika? Apakah suatu yang tidak real? Hanyakah ngoyoworo ataukah hanyakah khayalan orang? Apakah seperti aljabar abstrak itu suatu yang mengada-ada saja ataukah memang harus menuju ke situ?

    Berikut semoga bisa memberi gambaran akan pemahaman tersebut. Sebagai langkah-langkah sebelum ke abstrak, kita berkecimpung dengan aritmatika yang di dalamnya ada proses seperti penjumlahan, perkalian, dan ada penggunaan variabel. Pengenalan abstrak di SMA biasanya dimulai dengan pelajaran induksi matematik dimana harus membuktikan keteraturan sampai tak hingga dengan membuktikan implikasi  P_k--->P_k+1 dan membuktikan P₀ benar.
     Waktu kita melangkah dari perhitungan dasar ke penggunaan variabel, kita meluaskan orientasi kepada cakupan perhitungan yang lebih luas. Kita bisa mengoperasikan bilangan-bilangan tanpa mengetahui berapa bilangannya, cukup dengan variabel. Nah ini, dari aritmatika menuju abstrak yang banyak membuat kepala para mahasiswa sakit, sebenarnya juga merupakan perluasan orientasi menuju semakin beragam dan semakin luas. Kita mulai dengan mempelajari sekelompok obyek, lalu interaksi antar obyek, yang lalu kita namakan operasi biner, mempelajari keteraturannya, mempelajari ciri-cirinya, lalu memformulasikannya menjadi aksioma-aksioma.

     Contoh di bawah mungkin bisa menjadi bayangan akan langkah tersebut, kita mulai dengan PENGANTAR TEORI BILANGAN.

Subgroup bilangan bulat
Kita perhatikan perhatikan himpunan bilangan bulat (integer), yaitu {...,-3,-2,-1,0,1,2,3,...} yang lalu biasa dinotasikan dengan Z. < huruf Z ini adalah diambil dari singkatan Zahl=bilangan dari Bhs Jerman>
Diberikan suatu himpunan bagian dari Z, katakanlah himpunan S. Himpunan S disebut subgroup dari Z jika memenuhi :
(i) x+y anggota dari S untuk setiap x dan y anggota dari S,
(ii) 0 anggota dari S,
(iii) -x anggota dari S untuk setiap x anggota dari S.

< catatan : Kalau pernah mempelajari tentang teori group, maka syarat-syarat di atas tidak lain sifat tertutup(i), ada elemen identitas(ii), dan untuk setiap anggota dari S yang bukan 0 punya invers. Di kasus bilangan bulat ini sifat asosiatif bisa dirunut dg mudah dari sifat tertutup >

Suatu himpunan bagian tak kosong S dari Z adalah subgroup jika dan hanya jika x - y anggota dari S untuk setiap x dan y anggota dari S.
Bukti :
S subgroup dari Z ==> x - y anggota S untuk setiap x,y anggota S
Karena y anggota dari S, maka -y anggota dari S
Karena x dan -y anggota dari S, maka x+(-y)=x-y anggota dari S
x - y anggota S untuk setiap x,y anggota S ==> S subgroup dari Z
Karena S tak kososng maka ada anggotanya, misalkan x anggota dari S, maka x-x=0 adalah anggota dari S , jadi 0 dan x anggota dari S sehingga 0-x=-x anggota dari S , lalu jika x dan y anggota dari S, sehingga -y anggota dari S, lalu x-(-y)=x+y anggota dari S . Terbukti.

Taruhlah m adalah bilangan bulat, dan kita buat notasi mZ={mn|n anggota Z}. Maka mZ adalah subgroup dari Z.

Teorema I
Jika S adalah saubgroup dari Z, maka S = mZ untuk suatu bilngan bulat tak negatif m. < dengan kata lain, teorema ini mengatakan bahwa kalau S adalah subgroup dari Z, maka pasti berbentuk himpunan kelipatan dari suatu bilangan bulat tak negatif {0,1,2,3,...} >
Bukti :
Kita buat dua kemungkinan, yaitu :
pertama --> jika S = {0}, maka dapat ditulis S=mZ dengan m=0.
kedua --> jika S tidak sama dengan {0}, atau S memuat bilangan bulat tak nol. Maka tentunya S memuat bilangan bulat positif < karena jika x anggota S maka -x juga anggota S >. Kita ambil misalnya m adalah bilangan bulat positif yang terkecil di S. Lalu suatu bilangan bulat positif n di S akan dapat ditulis dalam bentuk n=qm+r, dimana q adalah suatu bilangan bulat positif dan r suatu bilangan bulat yang memenuhi 0<=r. Dengan demikian r juga anggota S, karena r=n-qm. Karena diasumsikan m adalah yang terkecil, maka haruslah r=0. Jadi n=qm, dengan demikian n anggota mZ, yang berarti S=mZ. Terbukti.

Teorema tersebut mengatakan bahwa kalau sebuah himpunan yang anggotanya bilangan-bilangan bulat serta memenuhi tiga aksioma untuk subgroup di atas, maka tentulah anggota-anggota himpunan tersebut berbentuk kelipatan dari suatu bilangan bulat positif.

Faktor Persekutuan Terbesar
Definisi :
Taruhlah a₁,a₂,...,a_r adalah bilangan bulat, yang tidak semuanya nol. Faktor persekutuan dari a₁,a₂,...,a_r adalah suatu bilangan bulat yang membagi habis setiap a₁,a₂,...,a_r. Faktor persekutuan terbesar dari a₁,a₂,...,a_r adalah bilangan bulat positif terbesar yang membagi habis setiap a₁,a₂,...,a_r. Faktor persekutuan terbesar dari a₁,a₂,...,a_r dinaotasikan dengan (a₁,a₂,...,a_r).

Teorema II
Taruhlah a₁,a₂,...,a_r adalah bilangan bulat, yang tidak semuanya nol. Maka ada bilangan-bilangan bulat sebutlah u₁,u₂,...,u_r sedemikian hingga
(a₁,a₂,...,a_r)=a₁u₁ + a₂u₂ + . . . +a_ru_r
dimana (a₁,a₂,...,a_r) adalah Faktor Persekutuan Terbesar dari a₁,a₂,...,a_r.
Bukti :
Pembuktian teorema ini, pertama kita harus menunjukkan bahwa suatu himpunan S yang anggota-anggotanya berbentuk n₁a₁ + n₂a₂ + . . . +n_ra_r dimana n_1, n_2,..., n_r bilangan-bilangan bulat merupakan subgroup dari Z dengan menunjukkan terpenuhinya  3 aksioma di atas. Lalu setelah terbukti, maka karena
S subgroup Z, akan berbentuk mZ. Dengan kata lain bahwa setiap anggota S merupakan kelipatan dari m. Dengan demikian m adalah faktor persekutuan dari a₁,a₂,...,a_r. Karena FPB adalah faktor persekutuan, maka otomatis ada u₁,u₂,...,u_r sehingga (a₁,a₂,...,a_r)=a₁u₁ + a₂u₂ + . . . +a_ru_r. Terbukti.

    Kiranya, ini bisa menjadi gambaran bahwa yang namanya abstrak bukan suatu yang tidak aplikatif, melainkan adalah perluasan orientasi kita dalam memandang. Memang terlihat lebih sulit, karena kita mencoba menengok yang disebalik dari yang nampak.

by departement saintek

Read More

SALAM INTEGRASInya HIMATIKA “REAL”

Foto : Ka Haris Ismunandar (Ketua pelaksana Salam Integrasi)

Kali ini Penulis akan membahas tentang salam integrasi, berkaitan dengan postingan sebelumnya yaitu HIMSAM. Iya benar sekali !! Salam integrasi adalah Makrab outdoor kelanjutan dari acara HIMSAM.

Wah mendengar Makrab outdoor bikin tambah semangatnih. Apa sih makrab outdoor itu ? Seseru apasih acaranya ? Benar ga sih makrab itu menakutkan ? Apasih yang berbeda dari makrab sebelumnya?? Dan perntanyaan lain lain sebagainya ? Nah mau taukan.. Ayo simakk..

Salam Integrasi, seperti biasa ada kepanjangannya juga yaitu Satu Malam Interaksi Beragam Ekspresi. (Hemm, Jadi mikir… nama makrab tahun depan apalagi yaa....ckckck :D). Tergambar sedikit makrab kali ini dari namanya. Malam pada acara ini adalah berbeda dengan malam-malam sebelumnya, malam yang bermakna, malam yang penuh berbagai ekspresi dan juga penuh dengan warna, malam yang tak terlupakan PASTINYA, Begitulahkira-kira. Asiikkk... :D

Acara ini diadakan bertepatan pada tanggal 21-22 April 2012 dan seperti biasa bertempat di Lamdikada. Kenapa biasa di Lamdikada ??, mungkin salah satu alasannya adalah tempatnya dekat, kaka2 alumni mudah menjangkau tempatnya dan dengan alasan keselamatan Lamdikada itu tidak terlalu jauh dengan Kota sehingga kalau terjadihal yang tidak diinginkan pada Peserta ataupun pada panitianya sekalipun, bias langsung diantar kerumah sakit. Nah..Ternyata Semuanya sudah dipikirkan matang-matang oleh kaka2 panitianya, sippp kaka :D

Salam integrasi diadakan dua hari satu malam. Cukup lama untuk sebuah acara, apa aja sih kegiatan dari waktu yang panjang itu ?. Nah, makrab itu terdiri dari : materi, public speaking, sharing, presentasi prososal, pensi, (bakar jagung, jar ketuplak :D), game dan lain lain pokonya acara senang-senang deh.

Nah ini nih, yang biasa dipermasalahkan, dan yang selalu terbesit di kepala mengapa makrab itu harus ada, kegiatan yang melelahkan dan yang lain sebagainya. Berbagai macam pendapat dari teman-teman matematika dengan beragam jawaban yang beragam pula. Penulis pun mencoba untuk merangkum dan menjawab mengapa makrab itu harus ada??.Nah, Makrab itu harus ada karena, Pertama, untuk membentuk kader-kader Himatika “REAL”. Makrab itu sesungguhnya acara khusus untuk membentuk kader-kaderbaru atau pemimpin baru yang tangguh untuk ke.eksis.an Himatika “Real” selanjutnya. Kenapa selanjutnya ?? karena masih banyak yang perlu dilakukan, yang perlu dibenahi dan masih banyak pula tantangan yang kemudian pasti akan di hadapi oleh Himatika untuk Tahun-tahun kedepannya (siapa yo kira-kira penerus selanjutnya..?? :D). Kedua, makrab itu mengenalkan mahasiswa yang baru dengan lingkungan barunya yaitu kampus dan prodi matematka. Jelas sekali terlihat perbedaan antara mahasiswa baru dengan mahasiswa lama. Mahasiswa yang baru masuk ke bangku perkuliahan, barang tentu semuanya masih terlihat canggung dalam hal apapun mengenai kampus baik dari segi mengatur waktu, pelajaran baru, teman baru,kaka baru, guru baru dan lain sebagainya, Mahasiswa baru mungkin akan mencoba beradaptasi dengan hal ini,namun pastinya akan berlangsung lambat. Nah, Makrab mampu membuat adaptasi ini berlangsung dengan cepat. Dan yang ketiga, yang paling penting dari sebuah makrab itu adalah makrab itu mampu mengakrabkan kaka tingkat dan adik-adik tinngkatnya, seperti tak di sangka-sangka ternyata setelah acara makrab ini selesai, terjalin sebuah ikatan baru, hubungan persahabatan baru antar mahasiswa matematika, baik dari kaka ke adiknya maupun dari adik ke kakanya, maka terciptalah sebuah kesolidan dan keharmonisan di dalam keluarga besar Himatika “Real” (Ciee… Ujung ujungnya untuk Himatika jua.am :D).Ehmm2… tak mampu lagi berucap, sebenarnya masih banyak lagi manfaat dari makrab ini, tapi takutnya tidak cukup halaman untuk hanya membahas dari manfaat makrab itu sendiri. (Padahal, alas an penulis ja..supaya kada lapah mengetik :D)

Ehmm. Setelah panjang namun tak lebar menjelaskan apa itu makrab “-_-. Ayokk sejenak, kita perkenalkan ketua pelaksana dari Salam Integrasi ini. Dia adalah Kaka angkatan 2009 berwajah manis, memliki tubuh tinggi sedang, coordinator departement SEGA dan jugaHumoris. Hayooo siapa yang tahu ?? Iyaa benarr sekalii,, Ka Haris Ismunandar. Prokkprokprok :D. Setelah ngobrol panjang lebar dengan Ka Haris, hanya termuat harapan dari kaka ketua pelaksana kita kali ini, hehehe

Saya : Ada Pesan-pesan lah ka untuk peserta makrab ?

Ka Haris : Ada dnk, Diharapkan semua ikuti acara itu dengan baik, jalani acara dengan ikhlas, jaga kesehatan selama acara karena kita disana menginap.

Saya : Ka, apa harapan kaka untuk acara makrab kali ini ?

Ka Haris : Mudahan, acaranya sukses (Amin :) ), Selamat (Amin :) ) Adik Mahasiswa bias akrab dengan kaka tingkat (Amin :) ), dengan dosen (Amin :) ), Berperilaku sopan dengan kaka tingkat dan dosen (Amin :) )dan bersikap sebagai Mestinya Mahasiswa. Aminnnn :)

Perhatian sekali kaka ketuplak kita ini,hehe. Iseng-iseng sedikit, penulis juga mencari beberapa pendapat dari kaka2 yang lain, ayo simak :D

Apa itu Makrab ??

Ka Ria Matik09 : Bakar-bakar jagung, menambah kebersamaan, melatih jiwa kepemimpinan, kekeluargaan dan dijamin peserta makrab ingin makrab lagi dan di jamin jagungnya masak :D.

Ka Lana Matik10 : Malam keakraban pnk :)

Ka Miki Matik10 : Makrab itu tempat berkumpulnya kating dengan ating, untuk apa yoo ?? :D. Intinya makrab itu rami banar tapi isuknya lapah dan tepar.Tapi rugi kada umpat makrab.

Ka Robi Matik10 : Kegiatan yang mengakrabkan angkatan baru dengan angkatan lama.

Jadi, sudahsedikit terjawab pertanyaan-pertanyaan paling atas tadi bukan. Nah ingin tau lebih jelasnya, ya nanti di.makrabnya aja langsung :D.

Seperti sudah tidak sabar lagi, acara Salam Integrasi ingin cepat-cepat di mulai.hehe

Nah, Besok lusa kita berangkat pagi-pagi sekali, mudahan acaranya ramee dan mudah-mudahan manfaat dari acara ini juga benar-benar terasa untuk kita semua kedepanya….. Aminnnnnn

by Departement Media Informasi

Read More

PARADOKS BANACH-TARSKI

Keanehan dalam matematika tidaklah sedikit. Dalam artikel ini diperkenalkan salah satu teori matematika yang menarik untuk kita ketahui. Teori ini berkaitan dengan salah satu objek dalam R³. Bisa dibilang ini adalah yang paling mustahil, paling aneh, dan paling ajaib dalam matematika. Menurut Paradoks Banach-Tarski, kita bisa memecahkan bola padat menjadi kepingan- kepingan berhingga kemudian menyusun ulang kepingan-kepingan tsb dengan menggunakan rotasi, dan translasi menjadi 2 buah bola yang identik dengan sebelumnya. Perlu dipahami bahwa bola padat yang dimaksudkan disini adalah bola padat menurut pemahaman matematika yaitu himpunan titik-titik tak hingga yang didefinisikan sebagai

dengan r jari-jari bola. Teori yang ditemukan oleh Stefan Banach dan Alfred Tarski ini melibatkan beberapa teori sebelumnya yaitu Translasi, rotasi, isometri, kongruen dan aksioma pilihan.

Paradox Banach-Tarski (PBT) dijelaskan dalam dua versi yaitu versi lemah dan versi kuat. Kedua versi ini memperlihatkan keanehan, dan keajaiban yang berbeda.

Versi Lemah

Proses PBT yang dijelaskan dalam versi ini mempertahankan: Bentuk, Ukuran, Kepadatan, dan Volume.

· Bentuk, artinya setelah proses PBT berlangsung bola padat yang dihasilkan sama seperti bola padat sebelumnya, tidak menjadi lonjong, gepeng atau setengah bola.

· Ukuran, artinya jika bola padat yang dipecah berjari-jari r, maka hasil PBT akan tetap berjari-jari r juga.

· Kepadatan, artinya untuk mendapatkan dua atau lebih bola padat yang memiliki ukuran dan bentuk yang sama dari susunan pecahan sebuah bola padat, tidak dilakukan peregangan, sehingga kepadatannya tetap.

· Volume, artinya tidak dilakukan penambahan material kepingan dari luar kepingan sebuah bola padat sebelumnya.

Untuk lebih jelasnya, perhatikan analogi berikut :

Secara formal, PBT Versi Lemah ini mengatakan,

Untuk sebarang bola padat

dapat dipecahkan menjadi kepingan-kepingan berhingga
dan isometri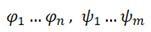
R³ sedemikian sehingga

Versi Kuat

Disini PBT hanya mempertahankan: Bentuk,dan Kepadatan.

Untuk volume dan ukuran tidak dipertahankan, namun bukan berarti versi ini tidak lebih aneh dari versi kuat. Untuk penjelasan mempertahankan bentuk dan kepadatan sama dengan di atas. Analogi berikut akan membantu Anda untuk menjadi lebih yakin bahwa versi ini memang pantas dikatakan versi kuat.

(sebuah kelereng)

=> (Matahari)

Sangat mustahil bukan ?

Percaya atau tidak, didunia matematika itu sangat mungkin dengan menggunakan PBT versi ini.

Versi kuat PBT mengatakan,

Untuk sebarang dua bola padat A dan B dengan
maka dapat dipecah menjadi kepingan-kepingan berhingga
dan

sedemikian sehingga untuk setiap i dari 1 sampai n,A_i kongruen dengan B_i. Perlu diketahui bahwa PBT ini tidak berlaku di R dan R². Dan beberapa literature mengatakan bahwa PBT akan dapat terjadi jika banyak kepingan tidak kurang dari 4 kepingan.

by Departement Saintek

Read More